The Surprising Persistence of Bad Signals

How likely is a debtor to default on a loan? How likely is a student to succeed in college?

Both of these questions demand a probability that is impossible to measure directly. Instead, we find signals that proxy for them. SAT scores are meant to predict college success. FICO scores proxy for creditworthiness. We accept that there is a certain amount of measurement error in these scores.

If the market for these signals operated like markets for other things (say, lawnmowers or laundry detergent), we would expect that over time better signals would emerge and replace the existing ones. Over a long enough time horizon, a lawnmower that is clearly better will run an inferior incumbent out of the market. Likewise, a significantly superior creditworthiness signal should eventually overtake competitors.

Instead, I will show that even ignoring switching costs and other sources of market friction, the market for signals doesn’t behave this way. There is a game-theoretic reason that even in an idealized free market, there can be strong pressure to use the signal that is already prevalent rather than a superior signal.

To demonstrate this, let’s pretend that we are installing a gumball machine. It takes one coin and dispenses one gumball.

We happen to know that in the location we’ve picked, a significant number of the coins in circulation are counterfeits.  Many of the counterfeits have manufacturing defects that reveal them as fake: 50% have a measurable size difference, and 80% have a detectible difference in conductivity. These errors are independently distributed, so a coin with a size defect is just as likely to have a conductivity defect as a coin without a size defect. So, if we select 100 counterfeits at random, we would expect the defect distribution to break down like this:

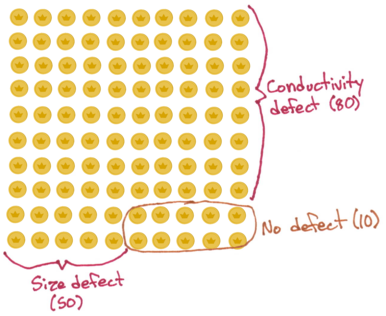
Let’s say there are two competing counterfeit detectors on the market, one which tests the coin’s size and another which tests the coin’s conductivity. Due to space constraints, we only have room for one. Both are perfect at detecting the manufacturing defects when a coin has them.

It should be pretty obvious that, all else being equal, the conductivity detector is the better choice. But here’s the rub: we’re installing the gumball machine in an location with four other candy dispensers. I happen to know that they all use the size method of detecting counterfeits. You have also observed that customers have a uniformly random ordering of preference over the machines, and they stubbornly try every dispenser in order of their preference when their coin is rejected.

Under these new circumstances, which counterfeit detector should we install?

Let’s say we pick the size method.

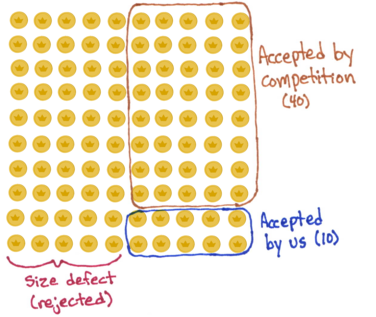
On average, out of 100 counterfeit coins, half will have a size defect – we can ignore those coins because our counterfeit detector will reject them. Of the half that we can’t detect, a fifth will belong to customers whose first choice is our gumballs (remember, there are four other machines and preferences are uniformly distributed). A fifth of a half of 100 is 10 coins, which is how many counterfeits we accept using this approach. (Since we never reject authentic coins with either method, I’m only considering how many counterfeits we accept.)

Now, let’s consider the conductivity method, again looking at an average 100 counterfeits.  

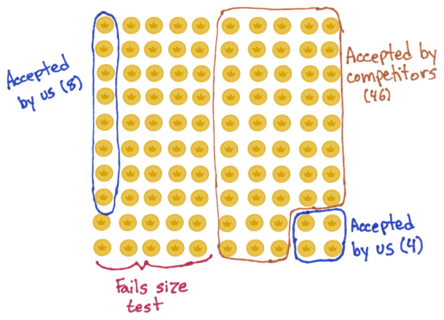
One fifth of the counterfeits will come to us first, as above. Of those 20, all but 4 are rejected by the conductivity test. But recall the stubbornness of our customers: when their coin is rejected by the size-based detectors, they will eventually find their way into our machine. We can reject 80% of them, but that still leaves us accepting an additional 8 counterfeit coins for a total of 12. Note that our competitors are worse off too: of the coins our machine rejects for failing the conductivity test, 6 will still pass the size test and end up at our competitors.

So to recap, the size method left us accepting 10 counterfeits, and the conductivity method has us accepting 12. This seems unintuitive, because the conductivity method is far superior!

This is just an instance of adverse selection, but it shows that we should be skeptical of the free market’s ability to select good proxies for signals of risk. I’ve glossed over some of the mechanics at play in a real market, but I do think the same phenomenon explains why there tends to be crowding around certain signals and an apparent lack of innovation.